Ex 96, 7 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑥𝑙𝑜𝑔𝑥 𝑑𝑦/𝑑𝑥𝑦=2/𝑥 𝑙𝑜𝑔𝑥 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q xlog x 𝑑𝑦/𝑑𝑥 y = 2/𝑥 log x Dividing by x log x, 𝑑𝑦/𝑑𝑥𝑦" × " 1/(𝑥 log𝑥 ) = 2/𝑥 𝑙𝑜𝑔 𝑥" × " 1/(𝑥 log𝑥 ) 𝑑𝑦 Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThis problem has been solved!
If Log Xy 3 1 2 Logx Logy Then Find The Value Of X Yy X
If log(x y/2)=1/2(logx logy) prove that x=y
If log(x y/2)=1/2(logx logy) prove that x=y-See the answer A) If log (xy/3) = 1/2 (logx logy), show that x^2 y^2 = 11xy B) Show that sin^2x cos^2x = 1 for pi/3Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Log Properties
Get answer If x^2y^2=27xy, then show that log((xy),(5))=1,2logxlogyIf $x > y$, can you prove $x \ \log y > y \log x$, where $x \ge 1$ and $y \ge 1$ I encountered this problem in a paper I read and somehow cannot prove itSolve for x log of x=y log(x) = y log ( x) = y Rewrite log(x) = y log ( x) = y in exponential form using the definition of a logarithm If x x and b b are positive real numbers and b b ≠ ≠ 1 1, then logb (x) = y log b ( x) = y is equivalent to by = x b y = x 10y = x 10 y = x Rewrite the equation as x = 10y x
Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeBy default, mathlog \ x/math would have a base of 10, so mathx = 10^y/math In general, in the equation mathy = log_b \ x/math, where b is the base, mathx = b^y/math If x = e^cos2t and y = e^sin2t , prove that dy/dx = ylogx/xlogy asked in Limit, continuity and differentiability by Raghab ( 504k points) differentiation
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Prove #x^(log_10(y)log_10(z))y^(log_10(z)log_10(x))z^(log_10(x)log_10(y))=1# Use the base 10 logarithm on both sides #log_10(x^(log_10(y)log_10(z))y^(log_10(zGet answer If x^(y)=e^(xy), prove that (dy),(dx)=(logx),((1logx)^(2))




Log X Y 5 1 2 Log X Log Y Show That X Y Y X 23 Brainly In




If X Y 7xy Then Show That 2log X Y Logx Logy 2log3 Logarithms Mathematics Problem Ms003 Youtube
Here we have to use implicit differentiation As log(xy) = x2 y2 or logx logy = x2 y2 assuming base is e, we have on differentiation 1 x 1 y dy dx = 2x 2y dy dx or dy dx (2y − 1 y) = 1 x −2x or dy dx = 1 x −2x 2y − 1 y = y − 2x2y 2xy2 −x In case base is 10, we can write it as lnx ln10 lny ln10 = x2 y2X^2 y^2 = 23xy => x^2 y^2 2xy = 25xy => ( x y )^2 = 25xy => x y = 5 (xy)^1/2 So , taking log both sides , /5 = 1/2 ( logxy) log(xy)/5 = 1/2(logx logy ) Hence$\begingroup$ I figured if I multiplied both sides by 5 $2^y5 = 4^x5$ I would have $10^y = ^x$, then $\log y = ^x$ as you can see that didn't actually help me $\endgroup$ –




If Logx Logy Log X Y Then A X Y B X Y 1 C Y X 1 X D




If Xy Log X Y 1 Prove That Dydx Y X 2y X Y X Xy 2 X Y
The equation 2 lo g 2 (lo g 2 x) lo g 1 / 2 lo g 2 (2 2 x ) = 1 has View solution If lo g 2 = 0 3 0 1 0 and lo g 3 = 0 4 7 7 1 , then the value of lo g 2 4 will beradg8 and 125 more users found this answer helpful If yx = eyx, then prove that \(\frac{dy}{dx}=\frac{(1log\,y)^2}{log\,y}\) Consider the function y = x^x √x 1Express the above function as logy = (x 1/2)logx 2



Log Properties



Www Worldscientific Com Doi Pdf 10 1142 0017
X square y square=23xy,prove that log xy/5=1/2(log xlog y) Get the answers you need, now! If xy = ex y, then prove that dy/dx = (log x)/(1 log x)2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesLog{{xy}/3}=1/2{logxlog Y} log(xy) log(3) = 1/2(log xy) log(xy) log(2) = 1/2(log xy) 2xy 4 = xy xy = 4 now x/y y



Www Worldscientific Com Doi Pdf 10 1142 0017
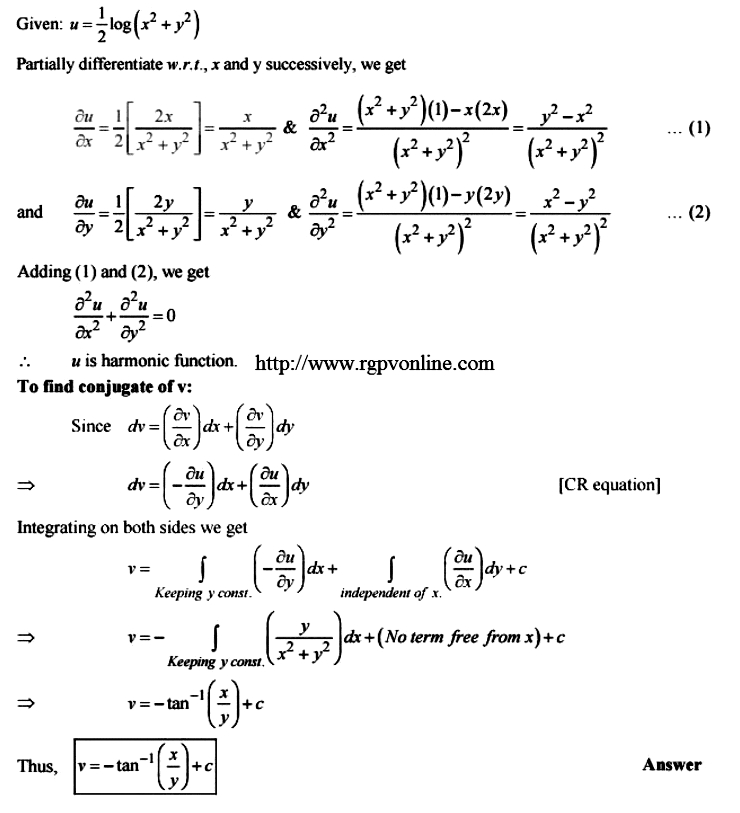



Show That The Following Function U 1 2 Log X 2 Y 2 Is Harmonic And Find Its Harmonic Conjugate Functions Mathematics 2 Question Answer Collection
You can put this solution on YOUR website!Get answer If x^2y^2=7xy, then prove that log((xy),(3))=1,2(logxlogy)Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Logs Defn Laws Tys 1




If X 2 Y 2 7xy Then Show That 2log X Y Logx Logy 2log3
Click here👆to get an answer to your question ️ If y^x = e^y x then prove that dy/dx = (1 logy )^2/logy Join / Login > 12th > Maths > Continuity and Differentiability > Logarithmic Differentiation (d x d y ) 2 − x yLet's change the first equation to single log terms with no coefficients math 2\log(xy) = \log((xy)^2) = \log(x^22xyy^2) /math math \log(5) \log(xI suppose you understand that to solve you must have an equation that is an equal to sign If you ask how to solve logx/logy it makes little sense to me But then maybe you intend to inquire about the Logarithmic Identity Which I state here with




Diploma Engineering Mathematics Notes




If X2 Y2 14 Xy Then Prove That2 Log X Y 4 Log 2 Log X Log X
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreClick here👆to get an answer to your question ️ If xy log(x y) = 1, prove that dydx = y(x^2y x y)x(xy^2xy)Ch 1 Real Numbers, Exercise 155 If x^2 y^2 = 25xy, then prove that 2log(xy) = 3log3 log xlogyAP SCERT Mathematics Textbook, Pg 23CCE MODEL, AP/TG Cl




If Log X Y 2 1 2 Logx Logy Prove Thatx 2 Y 2 6xy Brainly In



How To Solve Log X Log Y Quora
4 log x y =logx−logy ProofToprove(1),fixyandcompute d dx logxy= 1 xy d dx (xy)= 1 xy y= 1 x = d dx logx x→0 logx=lim n→∞ log 1 2n 1exy=exey 2e−x= 1 ex 3 (ex)r=exr forrationalr ProofThisisleftasExercise4If you like this video then dont forget to subscribe to my channel for more videos if x^2y^2=10xy prove that 2log (xy)=logxlogy3log2 How to solve if x^2y^2=10xy prove that 2log (xy)=logxlogy3log2 I have a maths problem to solve, can anyone drop a paper solution for if x^2y^2=10xy prove that 2log (xy)=logxlogy3log2 Add a video to describe the problem better



If Log Xy 3 1 2 Logx Logy Then Find The Value Of X Yy X




If 2log Log X Y 5 Logx Logyshow That X Y Y X 27 Brainly In
Singhsaurav5600 Incredible29 Incredible29 Heya user Here is your answer !!To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `x^2 y^2 = 14xy and 2log (k (x y))=(logxlogy)`, then the value of k isRewrite in Exponential Form log of x=1/2 log(x) = 1 2 log ( x) = 1 2 For logarithmic equations, logb(x) = y log b ( x) = y is equivalent to by = x b y = x such that x > 0 x > 0, b > 0 b > 0, and b ≠ 1 b ≠ 1 In this case, b = 10 b = 10, x = x x = x, and y = 1 2 y = 1 2 b = 10 b = 10 x = x x = x




If Log X Y 7 1 2 Logx Logy Then Show That X Y 51xy Brainly In




Techniques Of Differentiation Further
The point of intersection is (10, 1/10), assuming the logarithms are in base 10 Isolate the logx in equation 1 logx = 2 logy Substitute for logx in equation 2 2 logy logy = 0 2 2logy = 0 2(1 logy) = 0 logy = 1 y = 10^1 y = 1/10 logx = 2 log(1/10) logx log(1/10) = 2 log(x/(1/10)) = 2 10x = 10^2 10x = 100 x = 10 The solution point is (10, 1/10) Hopefully this helps! If y = (sin x) x sin1 (x) 1/2, find dy/dx Mention each and every step find dy/dx y = (log x) x (x) log x mention each and every formula and minute details find dy/dx mention each and every formula and minute steps and detail Y = x x e (2x 5) Differentiate x sinx w r to x Differentiate (log x) cot x w r to xTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If log x logy log z = (yz) (zx) (xy), then




Partial Differentiation



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community
log (xy)/2 = 1/2 ( logx logy) log (xy) / 2 = 1/2logxy xy/2 = √xy xy = 2√xy Squaring on both sides; logx logy = 6 logx logy = 2 Now just solve as usual for logx and logy Then raise whatever base you are using (probably 10) to the respective powers 👍X²y²2xy =4xy x²y² = 6xy Hence proved !



How To Solve Log X Log Y Quora




If X Y 2 4a N D Log 3 Log 2x Log 1 3 Log 1 2 Y 1 Th
If x = e^cos2t and y = e^sin2t , prove that dy/dx = ylogx/xlogy asked in Limit, continuity and differentiability by Raghab ( 505k points) differentiationSimplify/Condense 1/2* log of x log of y log of z 1 2 ⋅ log(x) − log(y) log(z) 1 2 ⋅ log ( x) log ( y) log ( z) Simplify 1 2log(x) 1 2 log ( x) by moving 1 2 1 2 inside the logarithm log(x1 2) −log(y)log(z) log ( x 1 2) log ( y) log ( z) Use the quotient property of logarithms, logb (x)−logb(y) = logb( x y) log b ( xTrue, if you can calculate the discrete logarithm, then it would be easy But that's hard too, eg see Wikipedia for more details No series in y can yield x To see this, first note that, replacing y (x) by y (x)a_0, one can assume without loss of generality that a_0=0 Introduce the series A (u)=\sum\limits_ {n=0}^ {\infty}a_nu^n
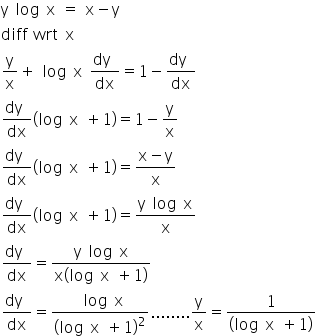



If Y Log X X Y Prove That Dy Dx Log X 1 Log X 2 Mathematics Topperlearning Com 2dolmeyy




If Log X Y 2 1 2 Log X Log Y Prove That X Y Brainly In
$\log{\Big(\dfrac{xy}{3}\Big)}$ $\,=\,$ $\dfrac{1}{2}(\log{x}\log{y})$ The left hand side expression is purely in logarithmic form but the right hand side expression is also in logarithmic form but the factor $\dfrac{1}{2}$ pulled us back in eliminating the logarithmic form from the equation




If X 2 Y 2 7xy Then Show That 2log X Y Log X Log Y 2log 3




Given Math 2 Log X Y Log X Log Y 2 Log 3 Math Show That Math X 2 Y 2 7xy Math Quora



If Log Y 2log 3x 1 1 How Do You Express Y In Terms Of X Quora



Search Q If 2 3 5ex 3d 0 23 5ey 3d1000 Then Find The Value Of 1 X 1 Y Tbm Isch




Proofs Of Logarithm Properties Chilimath




Question 4 A Rewrite The Equation 2 4 2 6 In Chegg Com




If Log X Y Log 2 1 2logx 1 2 Logy Then Youtube




Proof Of The Logarithm Product Rule Video Khan Academy



If Log X Y 2 1 2 Logx Logy Prove That X Y Brainly In




3 1 Properties Of Logarithm




If Log X Y Log X Logy Then Show That X Y 2 Y 1 Brainly In




If X Y 25xy Prove That 2log X Y 3log3 Logx Logy Youtube




If Log X Y Log5 1 2logx 1 2logy 0 Then X Y Y X Is Equal To




If X Y 27xyshow Thatlog X Y 5 1 2 Logx Logy With Using Formulaei Want It With Brainly In



Www Jstor Org Stable




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X Brainly In




X 3 Y 3 0 Prove That Log X Y 1 2 Logx Logy Log3 Brainly In



Prove That Xy Log Y C Is The Solution Of Dy Dx Y 2 1 Xy Xy 1 Sarthaks Econnect Largest Online Education Community




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




Log X Y 2 1 2 Logx Logy Novocom Top




If X Y Y X 23 Prove Log X Y 5 1 2 Log X Log Y Maths Meritnation Com
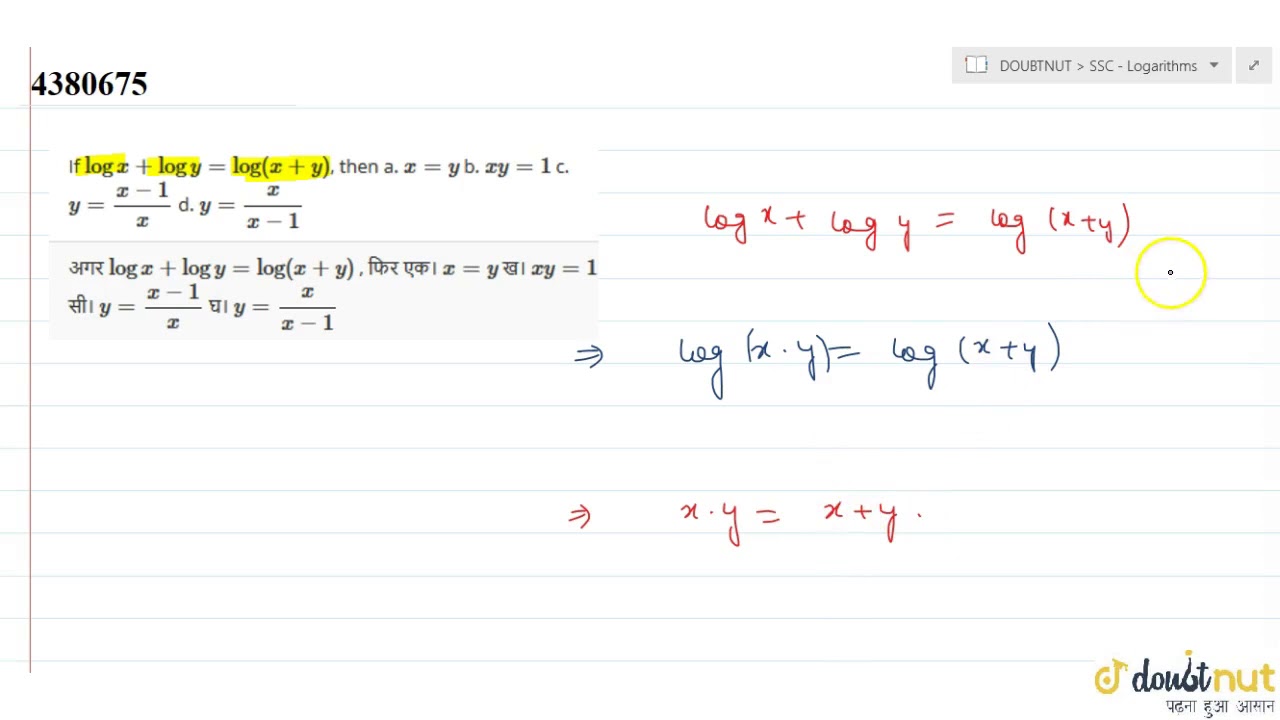



If Logx Logy Log X Y Thena X Y B X Y 1 C Y X 1 X D Y X X 1 Youtube




If Log X Y 5 1 2 Log X Log Y Show That X 2 Y 2 27 Xy Brainly In




Ib Hl Math Homework 2 Logs Binomial Theorem And Induction




If Log X Y 2 1 2 Logx Logy Logz Then Find The Value Of X Y Y X Mathematics Topperlearning Com 9g3iizyy



5 Derivative Of The Logarithmic Function



If X 2 Y 2 7xy How Do You Prove That 1 2 Logx Logy Log X Y 3 2 Quora




If Log X 2 Y 2 Tan 1 Yx Then Prove That Dydx X Yx Y




If X 2 Y 2 6xy Prove That 2log X Y Logx Logy 3log2 Youtube



If Xy E X Y Then Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community




Log X Y 2 1 2 Logx Logy Novocom Top




If Log X Y Log X Log Y Then Show That X Y Y Y 1 Brainly In




Log X Y 3 1 2 Log X Log Y Show That X Power 2 Y Power 2 11xy Brainly In




Implicit Differentiation Advanced Example Video Khan Academy




If Log X Y 5 1 2 Logx 1 2 Logy Show That X 2 Y2 27xy Brainly In




If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1



If Log X Y X Y What Is Dy Dx Quora




Log X Y 2 1 2 Logx Logy Novocom Top



If F X Cos Log X Then F 1 X F 1 X 1 2 F X Y F Xy Is Equal To Sarthaks Econnect Largest Online Education Community




Derivative Of X 2 Y 2 Log Xy Youtube




If X 2 Y 2 14xy And 2log K X Y Logx Logy Then The Value Of K Is Youtube




Proofs Of Logarithm Properties Video Lessons Examples And Solutions



Proof Of Log Xy Log X Log Y Mathematics Stack Exchange




How To Prove That Math Yz Log Y Log Z Cdot Zx Log Z Log X Cdot Xy Log X Log Y 1 Math Quora




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X




Ml Aggarwal Solutions For Class 9 Chapter 9 Logarithms Get Free Pdf




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If X Y 27xyprove That Log X Y 5 1 2 Logx Logy Brainly In



Q Tbn And9gctf6o7qan9knytzw4az39fwsy9z Dgqnpo0yqiaiomfbffpoi Usqp Cau




If Log Xy 3 1 And Log X 2y 1 Then The Value Of Xy Is Equal




X Y Y X 14 Then Prove That Log X Y 4 1




If Y X 2 1 Log X 2 1 X Show That X 2 1 Dydx Xy 1 0
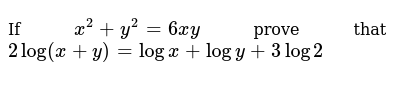



If Log X Y 2 1 2 Log X Log Y Prove That X 2 Y 2 2xy
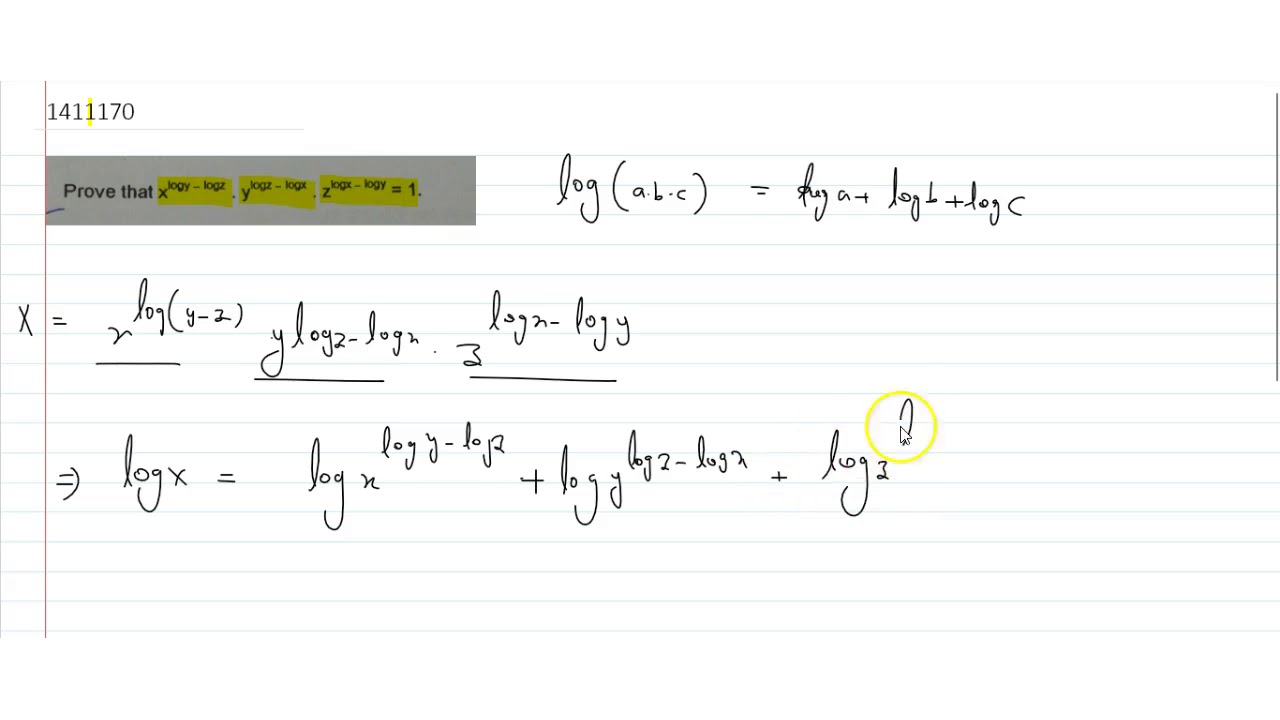



Prove That X Logy Logz Y Logz Logx Z Logx Logy 1 Youtube




If X 2 Y 2 7xy Then Prove That Log X Y 3 1 2 Logx Logy




If Log X Y 3 1 2 Logx Logy Find The Value Of X Y Y X Class 10 Youtube
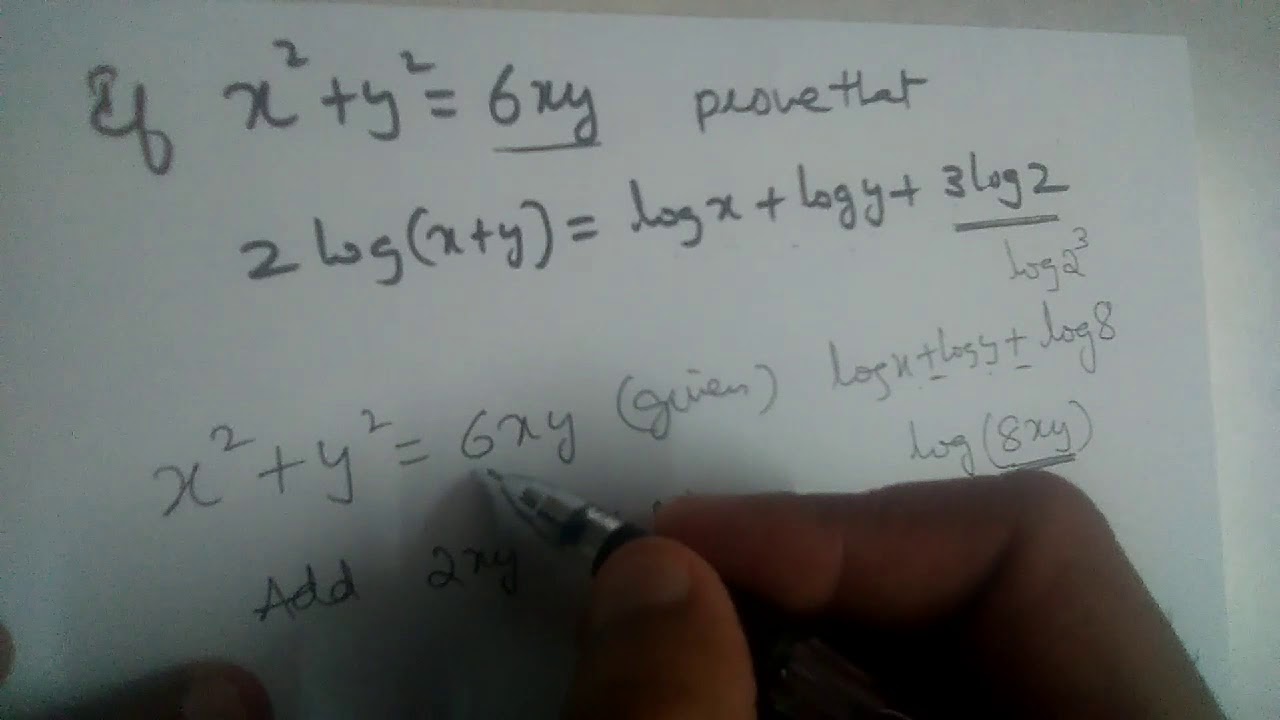



If X Y 6xy Prove That 2log X Y Logx Logy 3log2 Youtube
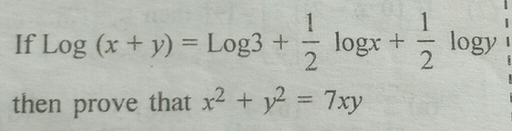



Begin Array L Text If Log X Y Log 3 Frac 1 2 Scholr



If Yx Ey X Prove That Dy Dx 1 Log Y 2 Log Y Studyrankersonline




Log X Y Novocom Top



How To Solve The Simultaneous Equation Xy 2 2log X 1 Log Y Quora
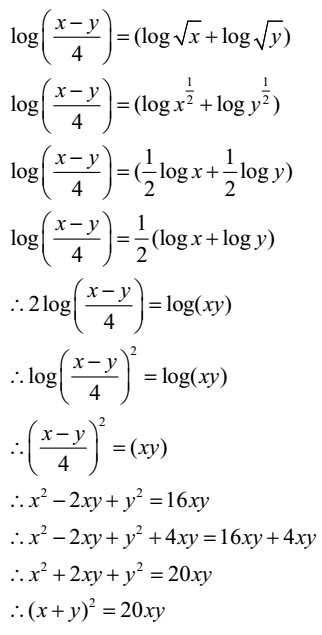



To Find Logarithm Archives The Fact Factor




Ex 9 6 6 Find General Solution X Dy Dx 2y X2 Log X



Proof Of Log Xy Log X Log Y Mathematics Stack Exchange




Selina Chapter 8 Logarithms Icse Solutions Class 9 Maths



How To Solve The Simultaneous Equation Xy 2 2log X 1 Log Y Quora




If Log X Y Z Logy Z X Logz X Y Then Prove That X



Let X And Y Be Two Real Numbers Such That 2ln X 2y Log X Log Y What Is The Possible Value Of X Y Quora
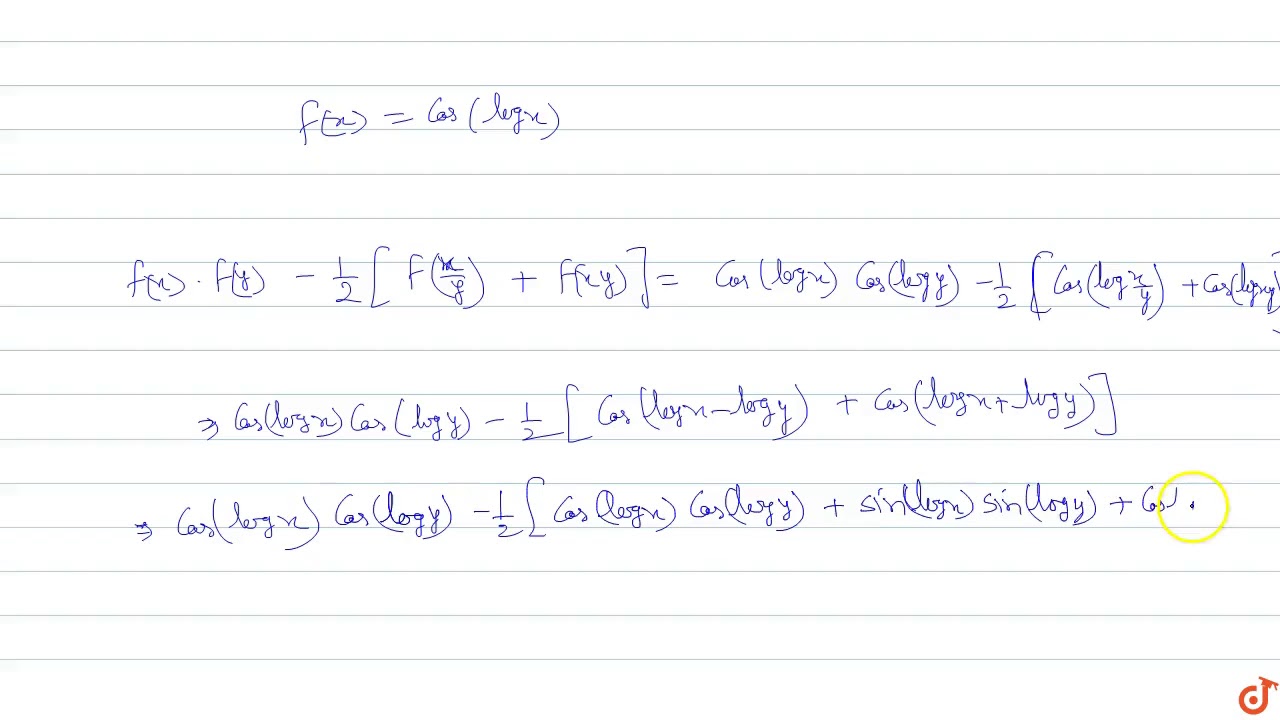



If F X Cos Logx Then F X F Y 1 2 F X Y F Xy Youtube




If Log X Y 2 1 2 Log X Log Y Prove That X 2 Y 2 6xy Brainly In
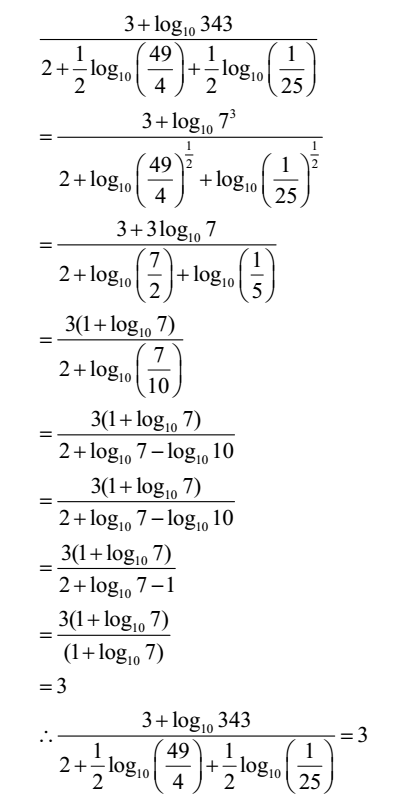



To Find Logarithm Archives The Fact Factor




If Log X Y 2 1 2 Logx Logy Find X Y Brainly In




Class 10 Real Numbers Mathematics If X2 Y2 25xy Then Prove 2log X Y 3log3 Log X Log Y Youtube




If X Y Log X Y 1 Prove That Dy Dx Y X 2y X Y X X Y




If X Y E X Y Prove That Dy Dx Logx 1 Logx 2




Simplify Log 1 X 1 Y Log X Y Logx Logy Youtube




If X Power2 Andy Power2 51xy Then Show That 2 Log X Y 2 Log 7 Log X Log Y Maths Real Numbers Meritnation Com




If X Square Y Square 27 Xy Then Show That Log X Y 5 1 2 Logx Logy Brainly In




Can U Solve These Problems 1if X To The Power 4 Y To The Power Of 4 47x Square Y Square Show That Log X Square Y Square 7 Logx Log Y
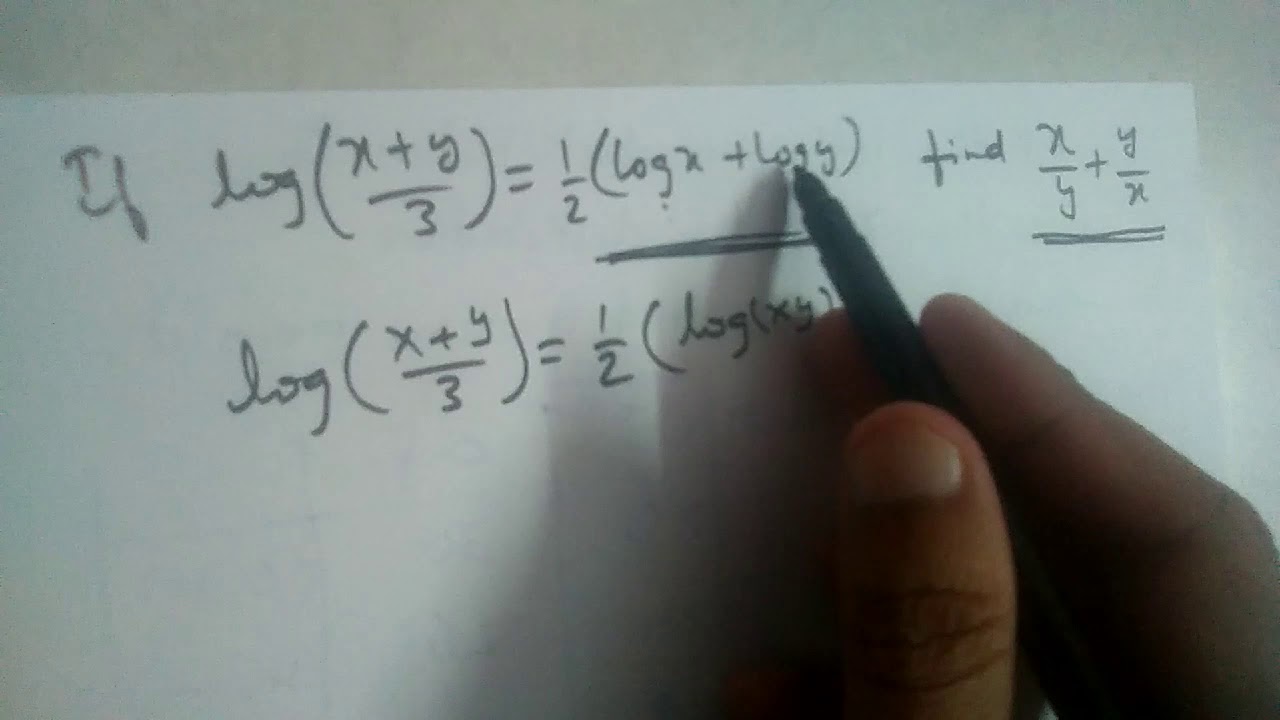



If Log X Y 3 1 2 Logx Logy Find The Value Of X Y Y X Youtube



0 件のコメント:
コメントを投稿